 |
 |
Introduction
C6H12O6 + 6 O2 ![]() 6 CO2 + 6 H2O
6 CO2 + 6 H2O
|
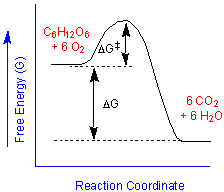
We can say that the combustion of glucose is "thermodynamically favorable", "energetically downhill" or "spontaneous", meaning that the energies of the products (carbon dioxide and water) are lower than the reactants (glucose and oxygen). Chemists typically depict such behavior with a free energy diagram such as that shown on the right. Provided that we supply an energy greater than the activation energy,
This diagram also tells us something that we might already recognize. If we run the reaction backward, we would have to surmount a higher
|  |
If we want carbon dioxide to participate in a chemical reaction without adding external energy, we need to find a reactant that has a high free energy or a product that has an even lower free energy to make the reaction favorable.
The reaction we are going to demonstrate here involves the extremely exothermic (heat evolving) and thermodynamically favorable reaction of magnesium metal (Mg) with carbon dioxide:
2 Mg(s) + CO2 ![]() 2 MgO(s) + C(s)
2 MgO(s) + C(s)
This reaction produces temperatures in excess of 2000 degrees C. If any oxygen is present during the reaction, the magnesium will react with it to form magnesium oxide, MgO, and the carbon dioxide would not react. Therefore, we need to find a way to exclude oxygen. We have a perfect way of doing that as you'll see in just a moment.
![]()
| Safety Notes: This demo involves burning magnesium and is inappropriate for some audiences and venues (elementary schools, for example). Burning magnesium demos have produced injuries and it is up to the lecture demonstrator to ensure that their audience is properly protected by distance, blast shield, experimental modifications and other means that are prudent for the venue selected by the demonstrator. This demo can only be performed indoors if there is adequate ventilation; keep in mind that MgO smoke is generated and can be a respiratory irritant and/or trigger smoke alarms. When performing this demo for an audience, one or more test runs should be made without spectators to ensure that all prudent safety considerations have been properly met. The reader assumes all risks associated with performing this demonstration and recognizes that this document can not anticipate all possible circumstances and does not guarantee that the procedures outlined herein are risk or hazard-free. |
The demo starts with a solid block of Dry Ice (frozen carbon dioxide). Recall that carbon dioxide sublimes at -78 degrees C, so proper cryogenic gloves must be used to prepare this demonstration.
| The first step is to cut the block in half. The best way to do this neatly is to make a thin saw cut and then use a wide masonry chisel. Alternatively, saw the whole thing in half. Using the chisel method this takes about two minutes. |  |
 |
The next step is to make hemispherical depressions approximately 6 to 8 cm in diameter in each piece. You can try doing this with a spatula, icepick etc., but it takes forever. If you use an electric drill and a large hole saw the process only takes about a minute for each cavity. |
| Important safety note: When the two halves of the block fit together "too well", this could impede the venting of evolved gases and lead to a "burp" that could potentially eject burning material. Therefore, it is important that one provide venting of the cavity. The easiest way to do this is to take a hand saw and make two perpendicular cuts about 1/4" to 1/2" deep across the faces of the blocks that will fit together. When the blocks are assembled, this gives four horizontal vent holes that are approximately the thickness of a pencil. Another benefit of the vent holes is that it makes the escaping vapors look more spectacular as they jet outward. | |
| Next, we place some magnesium turnings in the hole we made for the bottom piece. These turnings shown here are tarnished, but they worked OK (Mg powder is not recommended as it may burn too quickly and explode). A typical demonstration uses 6 to 8 grams of turnings for a large lecture hall. We have done up to 25 grams at a time, but the reaction produces a fairly significant mist that contains MgO. Be careful to do a small test run to see if your room's size, ventilation, audience, smoke detectors etc. will permit this demo to be run indoors. 25 g is definitely pushing one's luck for an indoor demonstration. |  |
 |
To get us over the activation barrier, we need to add a little heat. The fastest and easiest way to do this is to ignite the Mg with a propane torch. Place a safety shield between the block and your audience and then light the magnesium. As soon as it catches fire, quickly place the other half block on top. Be sure you orient the top beforehand so that the top fits correctly. (Important: provide the vent holes discussed above!). Turn out the room lights if doing this indoors. |
|
Click on the image at the right to view a QuickTime movie of the demonstration (you can download this for your platform if it is not already installed on your computer). The file is 654 Kb. The actual duration of the demo is longer than the 29 seconds shown here; we deleted some of the footage in the middle. The camera compensates for the incredible brightness of this demonstration (notice how the background disappears once the reaction starts). It is so bright that your audience should be warned not to stare directly at the block during the period of greatest intensity! |
|
 |
After the reaction has subsided, we are left with a chunk of material that looks like this. It has a coating of water ice condensation (remember the block is -78 degrees C), so let's scoop the residue into a weighing pan and examine it. |
| Now that the water ice condensation has melted and we have broken up the residue, we can see that the material consists of a white solid and a black solid. The black solid is the carbon we hoped to produce and, no, it does not contain any C60. The white material is the magnesium oxide. |  |
![]()
A few points worth mention here are:
That is a great question so let's examine it a bit further. First, let us calculate how much carbon dioxide is required for the reaction. If we use 16 g of Mg with a molecular weight of 24 g/mol, then we have (16 g)/(24 g/mol) = 0.66 mol of Mg. According to our balanced reaction above, we need half this number of moles of CO2 = 0.33 mol. Given a molecular weight of 44 for CO2, that is (0.33 mol)(44 g/mol) = 14.67 grams, roughly a half-ounce.
"Ah!" you say. "What about all the HEAT? Doesn't that melt the CO2?" Good question. Let's calculate how much thermal energy is released in this reaction. If we look at the standard state enthalpy values for the products and reactants we find they are:
| Component | |
|---|---|
| Mg | 0 kJ/mol |
| CO2 (g) | -393.5 kJ/mol |
| MgO (s) | -601.8 kJ/mol |
| C (s) | 0 kJ/mol |
Mg and C are zero because, by definition, the ![]() Hfo of elements in their standard states is zero.
Hfo of elements in their standard states is zero.
The ![]() H for this reaction is the sum of the
H for this reaction is the sum of the ![]() Hfo's of the products - the sum of the
Hfo's of the products - the sum of the ![]() Hfo's of the reactants (multiplying each by their stoichiometric coefficient in the balanced reaction equation), i.e.:
Hfo's of the reactants (multiplying each by their stoichiometric coefficient in the balanced reaction equation), i.e.:
![]() Horxn = (2 mol)(
Horxn = (2 mol)(![]() HfoMgO) + (1 mol)(
HfoMgO) + (1 mol)(![]() HfoC) - (2 mol)(
HfoC) - (2 mol)(![]() HfoMg) - (1 mol)(
HfoMg) - (1 mol)(![]() HfoCO2)
HfoCO2)
![]() Horxn = (2 mol)(-601.8 kJ/mol) + (1 mol)(0) - (2 mol)(0) - (1mol)(-393.5 kJ/mol)
Horxn = (2 mol)(-601.8 kJ/mol) + (1 mol)(0) - (2 mol)(0) - (1mol)(-393.5 kJ/mol)
![]() Horxn =-810.1 kJ
Horxn =-810.1 kJ
That is a fairly large free energy change. For comparison, the combustion of methane gas is -818 kJ/mol. We see that the thermodynamic driving force for this reaction is a) the high stability (low free energy) of the MgO that is formed and b) the reaction stoichiometry which forms two moles of this very stable substance.
Now, let's assume that all of the energy went into heat, even though we know that much of it went into making light. If we consume 0.33 mol of carbon dioxide in this reaction then that liberates (0.33)(810.1 kJ) = 267 kJ of energy that we can put into melting the carbon dioxide block.
The heat of vaporization of carbon dioxide is 571 kJ/kg. If we were to use all of our 267 kJ to a) vaporize the carbon dioxide b) not raise the gas temperature above -78 degrees (both of which are very generous assumptions; recall how much light we got) then the most we could possibly vaporize is (267 kJ)/(571 kJ/kg) = 0.47 kg or roughly one pound. The block weighs approximately 40 pounds, so this isn't a tremendous change in mass.
![]()
[Top of Page] [Demo Lab Home Page]
This page was last updated Friday, March 27, 2015 and is copyright 2001 by Rob Toreki. All rights reserved. Thanks to the late Terry Todd for his assistance in preparing the demonstration for filming. You are missed, friend.